ICGEM Service
Frequently Asked Questions (FAQs)
These questions are prepared as a collection of the frequently asked questions to the ICGEM Service. Some of the questions have both short and long answers. Users of ICGEM Service or interested readers who only need short clarification or description can refer to the short answers, whereas more interested users who would like to have more detailed description in physics and mathematical perspectives can refer to the long answers. Users who have any further question on the FAQs can get more information from the references listed at the end of this document and publications of ICGEM Service, and they can also contact the ICGEM team at icgem@gfz-potsdam.de. ICGEM is hosted and funded by Helmholtz Centre Potsdam, GFZ German Research Centre for Geosciences and any critics, comments, and suggestions to improve the ICGEM service and its content are welcome.
ICGEM FAQs (pdf)
Answer: The International Centre for Global Earth Models (ICGEM) was established in 2003 as a new service under the umbrella of the new International Gravity Field Service (IGFS). It has been an active web based service since 2003 and includes:
- collecting and long-term archiving of existing global gravity field models and solutions from dedicated time periods (e.g., monthly GRACE models)
- making global gravity field models available on the web in a standardized format (self-explanatory)
- the possibility to provide Digital Object Identifiers (DOI) to the models (i.e., to the dataset of coefficients)
- an interactive visualization tool of the static and monthly global models (geoid undulations and gravity anomalies)
- a web-interface to calculate gravity functionals from the spherical harmonic models on freely selectable grids (Gaussian filter in spatial domain included)
- a web-interface to calculate and plot the time variation of the gravity field at freely selectable positions or over defined basins → the G3-Browser (GFZ Grace Gravity Browser)
- the theory and formulas of the calculation service in Scientific Technical Report STR09/02 (downloadable)
- the comparison of the models in the spectral domain
- the comparison of the models with GNSS/levelling derived geoid values
- the visualization of surface spherical harmonics as tutorial
- the ICGEM web-based discussion forum
Short Answer: Gravitation is the attractive force between masses. The gravitational field of the Earth is a vector field and describes how the Earth attracts (magnitude and direction) other masses depending on their position relative to the Earth. The gravitational potential is a scalar field from which the attraction can easily be computed.
Long Answer: According to Newton's law of gravitation, the magnitude $F$ of a force between two masses $m_1$ and $m_2$ (which are assumed to be point shaped to make the formulation simple) depends on the two masses and the distance $l$ between them:
This attractive force is proportional to the masses and inversely proportional to the square of the distance between the masses. Therefore, the attractive force becomes bigger when the masses are bigger and it becomes smaller when the distance between the masses is larger, where $l^2$ in the denominator means that the force quadruplicates if the distance is divided in halfes.
The direction of the force is along the distance $l$ connecting the point masses. Hence the force is a vector:
Imagine the mass distribution of the Earth as a sum of many (say $n$) point masses $m_1, m_2, ..., m_n$, positioned at locations $q_1, q_2, ..., q_n$. Then, the resulting force of all these masses acting on a mass $m_p$, located at position $p$, is:
It is possible to define a scalar field $V(p)$ in such a way that the vector field $\vec{g}_a(p)$ can be derived from $V$ by its gradient:
This scalar field $V$ (equation eq:gravitation) is called the gravitational potential. If we know the gravitational potential, then we also know the gravitation. Because it is easier to handle the scalar field $V$ than the (3-dim.) vector field $\vec{g}_a$, generally the potential is used to describe the attraction of a body (See also question potential_negativ and heiskanen1967physical, or hofmann2006physical).
Short Answer: The terms gravity field and gravitational field are commonly mixed or used interchangeably. However, in geodesy, there is a difference between the two which is due to centrifugal potential.
Long Answer: The differences between the gravity field and gravitational field are given as follows:
Gravitational field is formed by the summation of pure attractive forces of the masses (of the Earth) (see question gravitational_field).
Gravity field is the sum of the Earth's gravitational attraction and the centrifugal force acting on the masses rotating together with the Earth (at the ground or in the atmosphere). Hence, the gravity potential $W$ is the sum of the gravitational potential $W_a$ and the centrifugal potential $\Phi$:
The sum of the gravitational acceleration (the gravitation) and the centrifugal acceleration is called the gravity vector or just gravity $\vec{g}$ and it can be derived from the gravity potential $W$ by computing the gradient:
A global model of the Earth's gravity field is a mathematical function which approximates the real gravity potential and allows to compute the physical quantities related to the gravity field, i.e., the gravity field functionals (see question functionals) at each position in the 3-dimensional space. A gravity field model therefore should contain both, a model of the gravitational potential and a model of the centrifugal potential. Because modelling the centrifugal potential is well-known and can be done very accurately, the relevant and challenging part of a gravity field model is modelling the gravitational field. Therefore, the term “gravity field model” is also very often used in the sense of “gravitational field model”.
Short Answer: The normal potential of the Earth should, on the one hand, approximate the real Earth's gravity potential for practical
purposes and, on the other hand, have a mathematical representation which is easy to handle.
By defining such a normal potential, the real gravity potential can be split into two parts, the normal potential $U$ and the disturbing potential $T$:
The normal potential together with the geometrical reference ellipsoid is called Geodetic Reference System (e.g., mularie2000department or moritz1980geodetic).
Long Answer: The normal potential is defined as follows:
- Like the gravity potential $W$, the normal potential $U$ also consists of a gravitational potential $U_a$ and the centrifugal potential $\Phi$: $U=U_a+\Phi$.
- One of the equipotential surfaces of the normal potential $U(x,y,z)$ is the reference ellipsoid. This means that this surface approximates the geoid which, in turn, is the equipotential surface of the real potential $W$ with the value $W_0$. The value of the normal potential on this surface is termed as $U_0$.
- The strength or intensity of the normal potential $U(x,y,z)$ is defined by postulating $U_0=W_0$ (which is equivalent to postulating that the mass generating the normal potential is equal to the mass of the Earth).
- the angular velocity of the Earth (usually denoted by $\omega$)
- the shape of the reference ellipsoid (e.g. its two semiaxes $a$ and $b$, or one of the semiaxes plus flattening $f$)
- the value $U_0=W_0$ (or, which is equivalent, the value for $GM$, the gravitational constant times the mass of the Earth)
Answer: The determination of the Earth's global gravity field is one of the main tasks of physical geodesy. Global gravity field models provide information about the Earth, its shape, its interior and fluid envelope. For instance, orthometric height and normal height systems are the most widely used systems in the world. These heights can be determined by traditional spirit leveling, a precise but inefficient method. With the contribution of satellite positioning and an accurate geoid model, the orthometric or normal heights can be determined at any point and at any time very efficiently (see also question geoid_height_anomaly). Obviously, the definition of a global height reference system is only possible with an accurate global gravity field model. If we speak about “heights above sea level”, we simply refer to the geoid as a reference surface which is accessible at any point globally. The geoid, in turn, is an equipotential surface of the gravity potential.
Also, time variations of global gravity field are essential in monitoring mass distributions all over the globe. Monitoring sea level variations, ice melting, ground water, drought severity in specific regions are only few of the common applications of time variable gravity field models.
Another important use of global gravity field models is the calculation of artificial satellites orbits. Considering hundreds of man-made satellites orbiting our Earth, without the contribution of a good global gravity field model, the calculation of the orbits precisely would not be possible.
Answer: All physical quantities that can be derived from the gravity field are called here gravity field functionals. For some of them, additionally, the knowledge of a reference system is necessary. There are functionals which are 3-D functions in the space outside the Earth, and there are functionals which are only dependent on latitude and longitude, therefore they are 2D functions.
3-D~functionals of the gravity field in ellipsoidal coordinates are the gravity potential $W(h,\lambda,\phi)$, gravity $\vec{g}(h,\lambda,\phi)$, gravity disturbance $\delta g(h,\lambda,\phi)$, gravity anomaly based on Molodensky's theory $\Delta g(h,\lambda,\phi)$, and generalized height anomaly $\zeta_g(h,\lambda,\phi)$. 2D~functionals are, the geoid (which is commonly given as undulations with respect to a reference ellipsoid) $N=N(\lambda,\phi)$ and the classical gravity anomaly $\Delta g(\lambda,\phi)$ (see, e.g., barthelmes2013definition).
Short Answer: There are different mathematical representations for gravitational field models, e.g., ellipsoidal harmonics, spherical radial basis functions, and spherical harmonic wavelets. In practice, almost exclusively, solid spherical harmonics are used to represent the gravitational potential globally. Therefore, model coefficients are spherical harmonic coefficients, which together with the spherical harmonic functions, approximate the real gravitational potential of the Earth.
Long Answer: A function, say $f(x)$, which is given by discrete measurements $f(x_j)=f_j$, and not continuously by a formula, is usually represented (or approximated), as a sum over so called basis functions $b_i(x)$ that are multiplied by coefficients $c_i$:
It is obvious that the choice of the basis functions depends on the type of the function which has to be approximated. Important is that the set of basis functions is sufficient to represent each function coming into question (which means, mathematically, the set of basis functions must be complete), and, that each basis function is really necessary, i.e., a basis function cannot be represented as a linear combination of other basis functions (which means, mathematically, the set of basis functions must be linearly independent).
Here, we want to approximate the global gravitational potential of the Earth, more precisely, the potential outside the Earth. From physics and mathematics, i.e., from potential theory, we know that this potential is not just an arbitrary 3-dimensional function outside the Earth, but, (because it has to do with potential energy) it fulfills some conditions. Particularly, it fulfills Laplace's equation:
Answer: The link for a list of models is provided on the main page: Models under “Table of Models” on the left. The user has an access to the model description as well as the coefficients on this list without any registration to the service. Model can be downloaded via clicking on the gfc (gravity field coefficients) or zip corresponding to the model listed under the Download column.
In more detail:
- Click on the link “Table of Models” on the navigation tab of our ICGEM-homepage. This opens a table with all global gravity field models.
- Go to the line with the model of your interest and click on the blue link labelled “gfc” in the column “download” with the left mouse button. This opens a new tab in your browser displaying the model gfc-file as text. Please consider that downloading models with high maximal degree can take some time, since they are quite large files. Therefore, it is preferable to download them as compressed files using the blue “zip” link.
- As an alternative, you can right click on the “gfc” and select the option “Save link content as...” to download the coefficient file and you can place it anywhere in your PC.
Answer: No, ICGEM does not compute the models. There are 158 models listed under the ICGEM Calculation Service at the moment. The list includes static gravity field models (e.g., satellite-only, satellite and terrestrial data combined models) as well as models from dedicated shorter time periods (e.g., monthly solutions) (see also question static_temporary). ICGEM accepts models from different institutes, universities, and research centres. Therefore, models come from different sources. The computation, estimation, and determination of the global models is not a task of ICGEM.
For further information about global models and their computation the reader is referred to barthelmes2014models (available here) and question harmonic_coefs.
Answer: ICGEM is a service for global gravity field models and not for gravity measurements. The service for gravity measurements is the Bureau Gravimétrique International. The different services of the geodetic and geophysical community related to the gravity field of the Earth are coordinated by the International Gravity Field Service - IGFS. Our service ICGEM offers the possibility to compute different functionals (e.g., gravity, gravity anomalies, gravity disturbances, or geoid undulations) from one of the global models on a grid of your choice (see the calculation service of ICGEM).
Answer: In geodesy, global gravity field model of the Earth, which is also called Global Geopotential Model is a mathematical function which describes the gravity field of the Earth in the 3-dimensional space. Due to mass redistribution on and inside the Earth (e.g., seasonal variations), the gravity field changes with time. Although these temporary changes are very small and/or very slow, they can be measured and modelled up to a certain degree.
A model, mean over a long time provides high resolution in spatial domain and no resolution in time domain. On the contrary, a model, mean over a short time (e.g., 1 month) provides low resolution in spatial domain and good resolution in time domain. There is a trade-off between the resolution in space and resolution in time. Hence, the long-term averaged models represent the mean value of global measurements, and describe static gravity field models. On the contrary, variations from dedicated time periods represent the variations of the gravity field corresponding to a specific (e.g., monthly) time period.
Answer: In physical geodesy, a gravity field model is used to approximate the real gravity field. If we could model the real gravity field perfectly, we would need infinitely many and perfectly determined coefficients so that our model would be equal to the real gravity field. However, in reality, this is not possible. We can determine a limited number of coefficients and try to approximate the real field as accurately as possible. At this point, the accuracy or error estimation of the model or model output needs to be investigated in terms of two errors, namely omission and commission error.
Omission error: Our approximation of the real field is NOT represented by infinite number of coefficients, but limited. The omission error occurs due to this limitation, in other words due to the truncation of the spherical harmonic series expansion at some degree (maximum degree). This process causes the terms above the maximum degree to be omitted, thus causing an omission error jekeli1979global. The omitted components have shorter wavelength than the resolution limit of the model and simply are not captured by the model.
Commission error: The other major error is due to the noise existing in the potential coefficients themselves. Since the limited coefficients cannot be determined perfectly, every single coefficient has an error component.
Moreover, determination of higher degree coefficients is subject to larger errors. The user can refer to one of the coefficients file to look at the error estimations of each spherical harmonic coefficients (columns 5 and 6) and notice that the estimated errors for higher degree and order coefficients are larger than the estimated errors of lower degree coefficients.
It is worth noting that the accuracy is related to a certain wavelength interval and differs for different wavelength intervals. The commission error increases as the maximum degree, $\ell_{max}$, of the spherical harmonic expansion increases (shorter wavelength interval), whereas the omission error decreases. Concerning the error estimation of a functional (e.g., geoid undulation) computed for a specific point, both the omission error and commission error of the model as well as their propagation to the functional should be considered.
Answer: Mathematically, resolution limit of a model (see also question resolution) in spherical harmonics depends on the highest degree and order of the model development. The real resolution in a specific region depends on the density and the quality of the data, that are included in the estimation of the model including the terrestrial measurements. EGM2008 is a combined model; therefore, satellite and terrestrial datasets are used in the development of the model. Accordingly, the error estimation of the model needs to be computed for each separately and then combined.
Combined model accuracy assessment can be performed via different techniques (e.g., internally and externally). One of the commonly used methods for the geoid undulation is to compare to external datasets, e.g., GNSS/leveling derived geoid undulations. However, the results provided by this technique are only as good as the GNSS/levelling data. Regarding the error estimation of a specific model internally, the user is referred to the authors of the model and the relevant web page (e.g., EGM2008).
Answer: Resolution of a model generally refers to the resolution in spatial domain. The length (e.g., size, dimension) of the smallest bump or dale which can be resolved, i.e., which can be captured and represented by the model, refers to the resolution of the model in spatial domain. In other words: how far away two very narrow bumps (in reality) must be, to be captured by the model as two separate bumps and not as one smoothed bump, is the limit of the resolution (see figure 5 in barthelmes2013definition). In a spherical harmonic model the resolution depends on the highest degree and order of the model and is very often defined as “half of the shortest representable wavelength” (or: shortest representable half-wavelength) that is captured by the model.
The maximum degree $\ell_{max}$ of the model expansion corresponds to the spatial resolution at the Earth surface by:
| spherical harmonic degree $\ell$ | half-wavelength $\psi_{min} [km]$ |
|---|---|
| 100 | 200.00 |
| 200 | 100.00 |
| 360 | 55.55 |
| 2190 | 9.13 |
This is the formal resolution which is mathematically possible using a model with maximum degree $\ell_{max}$. The real resolution, of course, depends on the data that are used to compute the model. Let us assume a combined model that consists of satellite measurements and terrestrial data. It is known that the satellite measurements are homogeneously distributed and have similar accuracy level in different regions. Contrary to that, coverage, quality, and accuracy of the terrestrial data that are included in the combined model vary from one region to another. Therefore, the resolution of the combined model also depends on the terrestrial data and differs from one region to another. Hence, if the terrestrial data are good, the model output can be as good as the formal resolution of the model. However, in other regions where no data or only limited bad data are available, then the regional resolution is expected to be worse than the formal resolution of the model.
Short Answer: Height anomaly is an approximation to geoid undulation according to the Molodensky theory, where the density of the topography above the geoid is not modelled.
Long Answer: Nowadays, with Global Navigational Satellite Systems (GNSS), it is possible to measure the coordinates of a point in space independently from the gravity field of the Earth, e.g., in cartesian coordinates, or, usually, with respect to a defined normal ellipsoid, i.e., in ellipsoidal coordinates (see also question normal_pot). Hence, also the height of a point can be defined with respect to the ellipsoid. But, ellipsoidal heights $h_t$ are not related to the gravity field and can not be used to derive where the water flows to.
The physical definition of heights related to the gravity field are the orthometric heights $H$, which are the heights above the geoid. The difficulty is that the geoid in continental areas lies inside the Earth and cannot be computed without knowledge about the density of the masses between the geoid and the topography.
Alternatively, heights can also be defined without any hypothesis about densities inside the Earth by normal heights $H^*$ which have been introduced by Molodensky (see heiskanen1967physical and moritz2000memoriam). In short, normal heights are an approximation of orthometric heights by approximating the Earth's surface by the so-called telluroid, and the real gravity field by the normal gravity field. The telluroid is the surface defined by $U_{telluroid}=W_{earthsurface}$ (see question normal_pot for the definition of normal potential $U$). Associated with this approach, the height anomaly $\zeta$ is the distance between the telluroid and the Earth's surface, see Figure fig:heights. For the ellipsoidal height $h_t$ of a point on the Earth's surface applies:
Answer: Unfortunately, the meaning of “zero degree term” is neither unique nor described well. We will start with the definition of the Earth's gravitational field and geoid, and how the geoid is calculated from the spherical harmonic coefficients of a gravity field model and explain the “zero degree term” and its use in geoid computation.
A spherical harmonic model of the Earth's gravitational field consists of the fully normalized unitless coefficients $C_{\ell m}$ and $S_{\ell m}$, a value for the geocentric gravitational constant $GM$, and a scaling factor $R$ which is generally equal to the equatorial radius of an adopted mean-Earth ellipsoid, and geocentric polar coordinates $(r_p, \theta, \lambda)$. For the model, $R$ is nothing more than a mathematical reference parameter. $GM$ is an essential part of the model. Multiplied by the coefficient $C_{00}$ (i.e. $GM * C_{00}$) it represents the gravitational constant times the mass of the Earth associated with the model, which means that $C_{00}$ (which is usually 1) scales the formal value of $GM$ that is given with the model. Additionally the tide system must be known (see also question tide_systems). By using these parameters, we can represent the 3-dimensional function of the geopotential $W(x,y,z)$ (outside the masses).
Geoid is one particular equipotential surface of the gravity potential of the Earth (Remember: the gravity potential is the gravitational potential plus the centrifugal potential). Among all equipotential surfaces, geoid is the one which coincides with the undisturbed sea surface and its fictitious continuation below the continents. If we knew the gravity potential $W$, we would know all equipotential surfaces. However, we do not know which one the geoid is. To calculate one particular equipotential surface of such a model we must define the potential value $W_0$=constant of this surface.
Geoid is usually given as geoid undulations or geoid heights with respect to a reference system which consists of a best approximating (in the least squares sense) geometrical rotational ellipsoid (normal ellipsoid) and an associated best approximating ellipsoidal normal potential $U = U(x,y,z)$. The defining parameters of such a reference system also define (implicitly by some formulas) the value of $U=U_0$ (ellipsoidal equipotential surface of the normal potential = geometrical ellipsoid of the reference system which approximates the Earth over the oceans). Moreover, the normal potential is defined in such a way that its value on the normal ellipsoid is $U =$ constant $= U_0$ and approximates the real value $W_0$ as good as it is known (at the time when this reference system is defined). Hence, the reference system also defines the value $W_0 = U_0$. By saying that, it is worth remembering that the improvement of the estimation of $W_0$ numerically is still under discussion and requires up to date information due to small changes of gravity field potential (e.g., sea level rise).
Following up the above discussion, we can simply say that zero degree term arises when $GM$ values between the geopotential model and reference ellipsoid differ and/or $W_0$ is chosen/calculated different than $U_0$. Therefore, this term needs to be properly accounted for to calculate the geoid undulation with respect to a known reference ellipsoidal surface correctly. ICGEM Calculation Service takes into account the $GM$ part and the geoid is calculated with respect to the reference system which is selected by the user. That means, the condition $W=W_0=U_0$ is fulfilled per definition with respect to this “user selected” reference system.
If we want to use an improved value of $U_0$, we think that it is better to change the reference system instead of adding a correction term afterwards. So, in our opinion, if you calculate geoidal undulations with respect to WGS84 and add a correction due to a different $U_0$, then the values belong to another reference ellipsoidal surface and do not belong to WGS84 anymore.
As mentioned above, the other part of the zero degree term is due to a possible difference of the $GM$ values between the Earth gravity constant of the gravity field model ($GM_{model}$) and the normal potential of the reference system ($GM_{ref}$). The zero degree term for the geoid undulation including both differences mentioned above can be computed as follows:
Answer: The difference between the geoid undulations computed with respect to the two systems is due to the different values $GM_1$ and $GM_2$ used in the ellipsoidal model (see question zero-degree). The geoid difference referring to these two reference systems can be computed by:
Answer: The different handling of the zero degree term is the reason for the differences between the “NGA EGM96 Geoid Calculator” and the ICGEM Calculation Service. Our philosophy is not to change any coefficients of the models including the value of $GM$ of the model and, therefore not to change the defining parameters of the reference system with respect to which the geoid should be calculated. The user have the option to include the zero degree term in the calculations on ICGEM “Calculation Service” that is computed based on different values of $GM*C_{00}$ of the geopotential model, and $GM$ of the normal potential, i.e., the reference system. Moreover, to use an improved value of $W_0 ( \neq U_0)$ we think it is better to change the reference system (such that $U_0 = W_0$) instead of adding a correction term afterwards. The user who would like to use their own reference system can use the option “user_defined ” in the calculation service of ICGEM.
For more detailed insight into this matter, the reader may refer to question zero-degree and to the nice article by Dru A. Smith at: http://www.ngs.noaa.gov/PUBS_LIB/EGM96_GEOID_PAPER/egm96_geoid_paper.html
Answer: There are three tide systems that are considered in the computation of a geoid model (see also, THE EGM96 GEOID UNDULATION WITH RESPECT TO THE WGS84 ELLIPSOID). The geoid in the three systems can be summarized as follows:
- Tide-free (or nontidal): This geoid is considered for a tide-free Earth with all (direct and indirect) effects of the Sun and Moon removed.
- Mean-tide: This geoid is considered in the presence of the Sun and the Moon (or, equivalently, if no permanent tidal effects are removed).
- Zero-tide: This geoid is considered if the permanent direct effects of the Sun and Moon are removed, but the indirect effect component related to the elastic deformation of the Earth is retained.
The transformation between the different tide systems in our Calculation Service only changes the coefficient $C_{20}$.
Answer: The 3D gravity field functionals explained in the answer to question functionals are computed by the Calculation Service at arbitrary heights above the ellipsoid. For the 2D functionals, we will continue with the geoid undulation example. Geoid undulation is defined as the distance between the geoidal surface and reference ellipsoidal surface. Therefore, it makes no sense to refer to any height or surface once again since the geoid height as well as the classical gravity anomaly and Bouguer anomaly are defined in 2D and height component is already involved in the definition.
Answer: Degree variances of the gravity field of the Earth correspond to the power (square of the amplitude) of the field for each wavelength. It is similar to the spectrum of a one-dimensional function. If the gravity field is represented in terms of spherical harmonics, the degree variances can easily be computed from the spherical harmonic coefficients and the spectrum can be given in terms of one of the gravity field functionals.
The error degree variance represents the noise characteristics of the gravity field for each wavelength and together with the degree variances it helps assessing the accuracy of the gravity field model. The user can refer to the following references for more detailed explanation and examples, Satellite Gravity and Geosphere in dickey1997satellite and Gravity An Introduction by Reiner Rummel.
Answer: The default values in the input mask of the calculation service are longlimit_ west $=$ 0° and longlimit_east $=$ 360°. The positive direction of the longitudes is eastwards. The keywords “longlimit_west” and “longlimit_east” of the input mask of the calculation service mean the following: The value for “longlimit_west” must be smaller than (or equal to) the value for “longlimit_east”. The longitudes can range from 0° to 360° (0° to $2\pi$) or from -180° to 180° ($-\pi$ to $\pi$), i.e., negative values are also allowed. If both values are negative, 360° will be added due to nature of the program coded.
Here are some examples:
- To produce a global grid one can enter the following values:
longlimit_west $=$ -180°
longlimit_east $=$ 180°
or
longlimit_west $=$ 0°
longlimit_east $=$ 360°.
However, in both cases the longitudes 0° $=$ 360° or -180° $=$ 180° are twice in the calculated grid (which is not necessary for plotting but it doesn't matter).
- For regional grids all combinations are possible as long as longlimit_west < longlimit_east:
longlimit_west $=$ 13.123°
longlimit_east $=$ 27.456°
or
longlimit_west $=$ -80$°
longlimit_east $=$ -60$°,
where the negative longitudes $-80$ and $-60$ will internally be changed to 280° to 300° in the grid file.
Short Answer: Time-dependent coefficients represent the time variations of the model (e.g., annual changes).
Long Answer: Our knowledge about the global gravity field (i.e., the accuracy of the global models) has become better and better and now it is possible to calculate not only mean models over a long period of measurements, but also time variations of the gravity field. Accordingly, the models from short time periods (one month or shorter) are also calculated and publicly available. However, these models have naturally lower spatial resolution due to the limits of short term observations.
As a result of combining mean models and models from monthly solutions, some additional parameters can be introduced to the mean model solutions. For instance, the models EIGEN-6S and EIGEN-6C contain, additionally to the (traditional) spherical harmonic coefficients, also some parameters which describe some basic time variations of these spherical harmonic coefficients. These additional parameters are the amplitudes of sine and cosine shaped time variations with annual and semi-annual periods as well as values for the linear trends of all coefficients up to degree and order 50. These new parameters are important, e.g., for exact orbit calculations or special investigations of time variations of the gravity field. If we want to calculate a functional from such a model, we have to know the epoch of interest. Then, in the first step, we use the formulas given in the header of the model to calculate the coefficients for this epoch. In the second step, we use the coefficients of this epoch in the same way as for the static models.
Answer: The software packages of the three analysis centres CSR, GFZ, and JPL are independent. However, they use the same data and data processing standards to generate the GRACE Level-2 products. Same processing standards (see also CSR Level 2 Processing Standards Release 5, GFZ Level 2 Processing Standards Release 5, and JPL Level 2 Processing Standards Release 5) here mean the common properties of the data processing (e.g., removing solid Earth tides and atmospheric effects from measurements). However, mathematical methods applied in designing measurement equations and techniques used in retrieving their solutions vary among the three centres and this results in different model coefficients.
The three centres release unconstrained solutions which means that no data external to GRACE measurements are involved nor any regularization (sometimes called stabilization) is used in the solution. As an advantage, users are free to develop their own filtering technique or apply the commonly used filters (also offered in the ICGEM Calculation Service) in order to remove the effects that come from the larger errors of high degree coefficients, and they do not have to start with data that are already filtered or modified. The disadvantage of the unconstrained models is the fact that the high degree coefficients have larger errors and they are not suggested to be used directly (without any filtering).
Answer:
a) Differences of monthly solutions (e.g., disturbance potential, geoid undulation) are caused by mass redistributions. Most of the effects are well-known (e.g., air pressure effects, tides) and can be modelled and removed from the measurements. Hence, the residual differences after eliminating the well-known effects are assumed to be mainly caused by water redistribution.
For example, if we take geoid differences between monthly solutions, in order to estimate how much the water stocks vary (increase or decrease in the amount of water), we need to modify our question into: How much water (Equivalent Water Height) is needed and how the distribution of the water should be in order to create that much geoid undulation difference between the monthly solutions?
b) The functional Equivalent Water Heights (EWH) is mainly used to interpret the differences of monthly solutions with respect to a mean model. Therefore, the EWHs are computed from the spherical harmonic coefficients of the monthly models minus the coefficients of a mean model (EIGEN-6, forste2012new). These difference-coefficients can be used after filtering or without filtering. The user should be aware of the high commission error (see questions accuracy and centres) in high degree coefficients if the unfiltered coefficients are used. The user can also select filtered coefficients in the Calculation Service.
For calculating the functional “water_column” (which means EWH) from a gravity field model the elastic deformation of the Earth due to the load of the water layer is considered. The exact formulas used in the Calculation Service for computing EWH from spherical harmonic coefficients of a gravity field model are described in wahr1998time and wahr2007time.
Answer: From point of view of ICGEM, it is not possible to say that the models from one centre are better (for some particular problem, e.g., hydrology) than the others. Best idea is to use the models from all the three centres and compare them. The monthly solutions of the three centres are produced unconstrained (see question monthly_models) and are provided without any filtering. Because, filtering characteristics depend on the specific application. Making decision of which filter to be used and how strong filtering is necessary, needs to be investigated and realized for each particular problem or application separately. Therefore, only the user can decide how to filter the monthly models.
ICGEM offers commonly used Gaussian filter in its Calculation Service. Using the Calculation Service, the user can apply the Gaussian filter immediately to the results of the computation. On the other hand, besides Gaussian filter, ICGEM offers de-correlation filters DDK on GFZ GRACE Gravity (G3) Browser. The user can use the pre-filtered coefficients to compute the equivalent water height or height anomaly via the G3 Browser.
Answer: Some of the gravity field models do not depend only on the spatial coordinates $(x,y,z)$ or $(r, \lambda, \theta)$ but also on time (see also question time_depend). A static model consists of the spherical harmonic coefficients $C(\ell ,m)$ and $S(\ell ,m)$ where $\ell$ is called degree, and $m$ is called order. The gravity potential $W$ (of such a static model) at a given position, $W(r, \lambda, \theta)$, is calculated by summing up over degree and order of a spherical harmonic expansion (see, e.g., equation 108 of the report: Theory).
For instance, in the model GOCO05S each coefficient (up to degree and order 100) has a static part, a linear trend with time and a sinusoidal time change with an annual period. If $G(t)$ is a coefficient, $C_{\ell m}(t)$ or $S_{\ell m}(t)$, its value for the time $t$ is:
It is worth remembering that the amplitude and phase of a sinusoidal wave with fixed period can be transformed mathematically into a sine-amplitude and a cosine-amplitude with the same period.
Answer: According to Newton's law of gravitation, gravity is always an attractive force. The closer an object with mass moves towards another object with mass, the larger the attractive force becomes. However, the definition of gravity potential is not unique. Gravity potential itself is not a quantity that can be measured directly, but the gravity potential differences can be measured. Accordingly, we can say that gravity potential can only be measured with respect to a reference potential, hence the nature of potential is that the zero point is arbitrary.
It is a convention in physics as well as in geodesy, and seems logical to set the potential “zero” at infinite distance. Now, imagine a mass at infinity, at “zero” potential. In physics, when the mass starts falling, it gains kinematic energy and loses potential energy. Therefore, the potential energy will decrease with respect to the start point which is at infinity. Hence, potential will decrease as the mass approaches the Earth. As a result, the potential is always negative and gravity $\vec{g}$ and potential $W$ are mathematically connected by:
Answer: ICGEM does not have any restriction on the submission of the models. Anyone can submit a model with the required minimum information provided along with model coefficients. Typically the author(s) can e-mail their model coefficients to icgem@gfz-potsdam.de in the .gfc format. It is recommended to include a header where the model characteristics (e.g. input data, a-priori information if used any, processing procedures, and references) are given (see also DOI landing page example). More details regarding the ICGEM format can be found in ICGEM format in detail. Please make sure the coefficients are in the correct format. Even though ICGEM performs standard quick-look assessments of the data and confirm that the model outputs do not produce any unnatural behaviour, this does not guarantee that the coefficient file is carefully checked. The authors are recommended to view one of the recent models to get familiar with the header and the format of the coefficient file as well.
In order to request a DOI number for the model coefficients, ICGEM asks the user to fill the Metadata Editor of GFZ Data Services first and submit the model to icgem@gfz-potsdam.de after receiving the citation and licence for the model and adding both information in the header of the data. An example XML file is available and can be loaded in the Editor and edited. A local copy can be saved via “Save as” and by clicking on “submit” the metadata will be sent to GFZ Data Services. The documentation of the Metadata Editor can be found via About/Help on top of the same page at Quick Start for Data Publication, GFZ Metadata Editor and Explanation for Metadata Fields. Filling the form with necessary information ensures the fast assignment of DOI number and publication of the model on ICGEM.
Short answer: Because positive topographic anomalies on Earth are mostly compensated by negative gravity anomalies in the crust.
Long answer: The total gravity field is composed of different parts: topography, ice sheets, ocean, Earth’s crust, and mantle. At first sight it might
seem strange that the observed gravity field, being the sum of all these components, has much smaller anomalies than one of its components, the topography. The
reason is that on Earth large positive gravity anomalies due to topography are underlain by large negative anomalies in the crust, and vice versa.
Take a large mountain belt such as the Himalayas. The weight of this mountain chain would cause the Earth’s crust to bend and material below the crust to move
down and sideways, causing the Himalaya to sink into the Earth over very long time (say hundred million years). Thus, a large mountain can only exist for
geologic time if it is supported by material of a low density with respect to the higher background mantle density. This principle is called isostasy, and is
similar to an iceberg in floating water: the weight of the iceberg above the water is supported by the part of the iceberg that is below the water, which causes
upwards force of the water because ice is less dense than water. The principle of isostasy for the Earth’s topography was formulated in the 19th century by Airy
and Pratt and others, triggered by measurements under leadership of Bouguer in the 18th century which showed much smaller gravity anomaly in the Andes than
expected based on the size of the mountains hofmann2006physical and WIKIPEDIA.
More information: The principle of isostasy requires that there is a material of lower density below the mountains, but what is it exactly?
In the case of the Himalayas, seismic measurements have shown that the Earth’s crust is thicker there. That means that in the bottom part of the crust, we have material with a density of 2700 $kg/m^3$ instead of a mantle density of 3300 $kg/m^3$ such as in a ‘normal’ part of the Earth. Compared to a reference Earth which is assumed to have a standard crust and mantle, we have a negative anomaly. Note that the reference Earth is crucial here, because it determines that we have positive and negative anomalies. However, it is not relevant what exactly the reference Earth model (e.g. ellipsoid, sphere) is. The reference Earth has no influence on the spatial pattern and spread in the topographic anomalies if you make a plot for part of the Earth, it will only shift, increase or decrease the anomalies by the same amount.
How can we calculate how much of the topography is compensated?
This is difficult to calculate since we do not know exactly what the Earth’s interior looks like. There are approximations, such as the Airy approximation which says that the weight of the topography is compensated exactly by making the crust thicker, or the Pratt approximation which says that the weight of topography is compensated by a locally less dense crust. Neither of these will be a perfect explanation for the real Earth, but of course they are useful for reducing the signal content before geoid modelling.
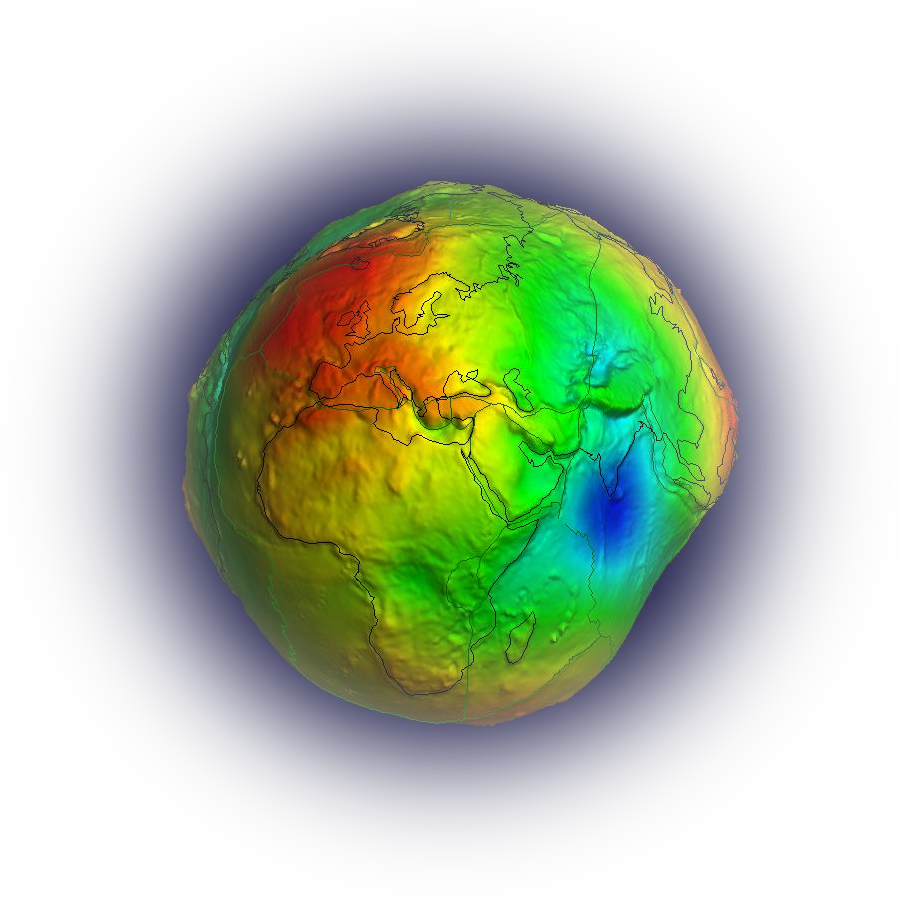


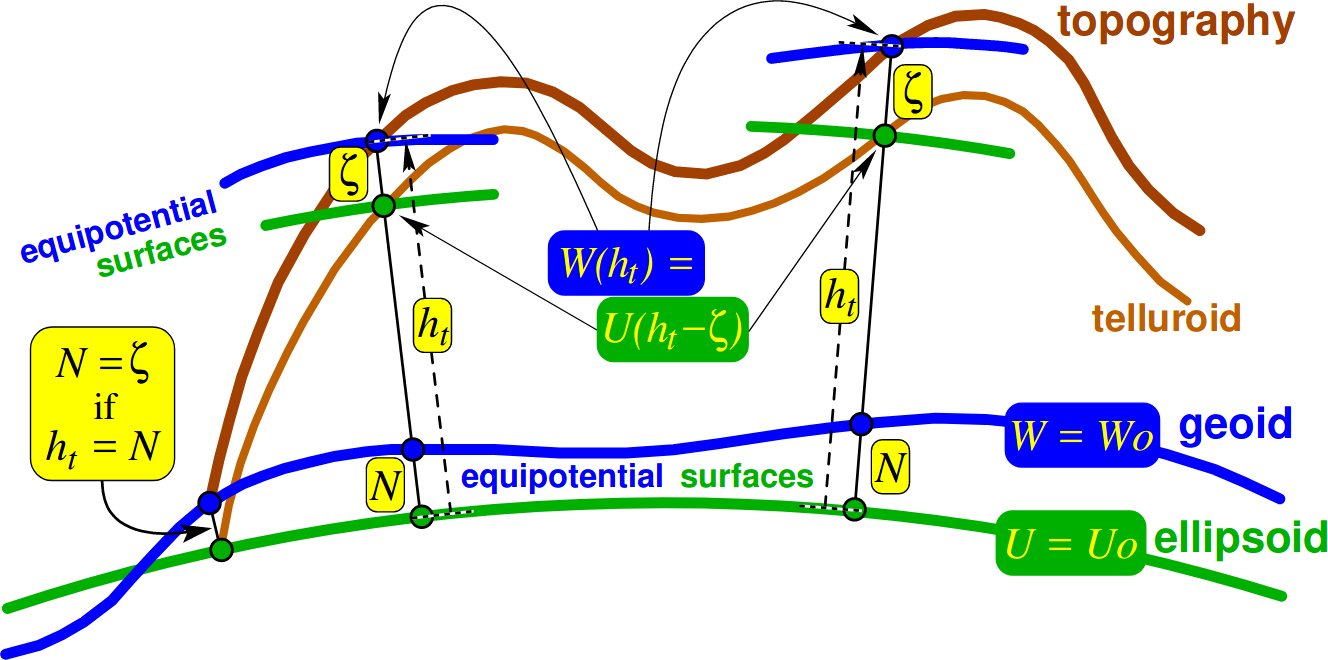 Figure 1: The ellipsoid, the geoid, and the height anomaly (taken from
Figure 1: The ellipsoid, the geoid, and the height anomaly (taken from